Ein wesentlicher Aspekt bei der Bewertung medizinischer Maßnahmen besteht in der Frage: Welchen Nutzen hat ein medizinischer Eingriff oder ein Medikament für die Empfänger?
Dazu werden in der Regel Studien durchgeführt, die anhand von Probanden versuchen herauszufinden, wie groß der Vorteil der Anwendung einer neuen Prozedur oder eines neuen Medikamentes gegenüber der Situation ist, wenn man das nicht tut.
In der Regel werden dazu zwei Gruppen gebildet: Zum einen die Gruppe derjenigen, die sich dieser Prozedur unterziehen oder das Medikament einnehmen (Studiengruppe) und zum anderen die Gruppe derjenigen, die das nicht tun oder wo nur so getan wird, als ob (Kontrollgruppe).
Anschließend werden die Ergebnisse gezählt und eine statistische Auswertung vollzogen. Ohne hier auf die näheren Details einzugehen, wie solche Studien aufgebaut sein sollten, bleibt natürlich am Ende die Frage der Bewertung des statistischen Ergebnisses.
Da eine rein theoretische Erklärung eher nur verwirren würde, werde ich hier an einem Beispiel eine solche „Erprobung“ einer neuen Operationsmethode simulieren.
Das Beispiel
Nehmen wir an, es gibt eine Erkrankung, die in jedem Lebensalter auftreten kann und bisher nicht zu heilen ist. Wenn Menschen daran erkranken, sterben sie mit einer Wahrscheinlichkeit von 10 %; das bedeutet also, dass von 100 Erkrankten 10 Menschen sterben werden.
Ein Chirurg, der sich damit nicht abfinden möchte, entwickelt eine Operationsmethode, um die Erkrankung zu heilen. Er findet 100 erkrankte Menschen, die bereit sind, sich dieser neuen Operationsmethode zu unterziehen.
Anschließend betrachtet er jeweils 2 Wochen nach dem Eingriff das Ergebnis und schreibt es auf.
Das Ergebnis sieht im Vergleich zu den Ergebnissen ohne die neue Operation folgendermaßen aus (Tabelle 1):

In der anschließenden Auswertung zieht er folgende Schlüsse:
Ohne Operation versterben von 100 Erkrankten insgesamt 10 Erkrankte (Kontrollgruppe); also 10 %.
Mit seiner Operation verstirbt von 100 Erkrankten nur 1 Erkrankter (Studiengruppe); also 1 %.
Um nun die Wirksamkeit seiner neu entwickelten Operation zu berechnen, kalkuliert er einfach das relative Verhältnis von 1 Verstorbenen der Studiengruppe zu 10 Verstorbenen der Kontrollgruppe: 1 / 10 = 10 %. Daraus schließt er eine Wirksamkeit von: 100 % (Ausgangswert Verstorbene Kontrollgruppe) – 10 % (Ergebnis Verstorbene Studiengruppe) = 90 % Wirksamkeit.
Die Schlussfolgerung des Chirurgen sieht daher folgendermaßen aus: Mit meiner neu entwickelten Operationsmethode gelingt mir eine Verbesserung der Prognose dieser Erkrankten um 90 %.
Fantastisch! Um diese große Chance nun breit anwenden zu können, muss er die neue Operation als gängige Methode zulassen; also letztlich von einem experimentellen Verfahren in ein völlig übliches Verfahren umwandeln. Dazu benötigt es eine offizielle Kommission.
Der Vorsitzende der Kommission sieht sich die Ergebnisse an. Er weiß, dass die Erkrankung für viele Menschen gefährlich sein kann. Daher ist es wohl sinnvoll, nicht lange zu zögern. Er beschließt gemeinsam mit den anderen Mitgliedern der Kommission, das Verfahren zuzulassen. Alle wissen, dass 100 Probanden nicht allzu viele sind, aber die Ergebnisse scheinen so eindeutig und die Wirksamkeit mit 90 % so hoch, dass Verzögerungen und Bedenken hier wohl nicht angebracht sind.
Daraufhin erfolgt die offizielle Zulassung der Methode und eine breite Anwendung derselben.
Einige Zeit und viele Tausend Operationen später zeigt sich jedoch leider, dass die Ergebnisse nicht halten, was man sich davon versprochen hat. Neben einigen Komplikationen des Eingriffes, an denen Erkrankte nach durchgeführter Operation sterben, scheint es so zu sein, dass operierte Patienten leider erneut an dieser Erkrankung leiden können und dann nochmals operiert werden müssen.
Relativ gegen absolut
Was ist passiert?
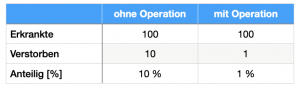
Leider hat die relative Betrachtung des Ergebnisses einen entscheidenden Haken: Sie vermittelt in vielen Fällen eine Wirksamkeit, die deutlich größer ist, als die absolute Wahrscheinlichkeit, eine Verbesserung zu erzielen. Schauen wir uns dieselbe Tabelle nochmals an, jetzt jedoch mit Angabe der Prozentzahlen (Tabelle 2).
Die absolute Verbesserung beträgt nur 10% – 1 % = 9 %. Was für ein riesiger Unterschied zu den 90 % aus der relativen Betrachtung! Noch einmal zur Verdeutlichung: Werden die Ergebnisse relativ zueinander gesetzt, dann ist der Unterschied mit 90 % riesig. Werden die Ergebnisse jedoch absolut miteinander verglichen, dann vermindert sich dieser Unterschied auf 9 % erheblich.
Aber was bedeutet das?
Leider ist nicht nur der Unterschied erheblich, sondern auch die praktische Konsequenz. Wenn ohne den Eingriff 10 von 100 Erkrankten sterben und mit dem Eingriff 1 von 100 Erkrankten stirbt, dann ist der Unterschied 9 von 10 Verstorbenen. Für diese 9 Verstorbenen, die durch den Eingriff gerettet werden könnten, muss ich aber 100 Menschen operieren. Anders ausgedrückt: Um einen Erkrankten zu retten, muss ich 100 / 9 = 11 Menschen operieren (die Zahl ist natürlich gerundet, exakt sind es 11,11). Diese Zahl ist eine aus der medizinischen Literatur gut bekannte Zahl: Es ist die sog. „number needed to treat“ (NNT); auf deutsch etwa: Die Zahl, die behandelt werden muss, um 1 Erfolg zu haben.
Wenn der Chirurg in unserem Beispiel aber nun bereits zu Beginn weiß, dass bei 90 % der Erkrankten die Erkrankung folgenlos ausheilt und „nur“ 10 % daran versterben, dann wird von den 11 Erkrankten, die er operieren muss, um einen zu retten, ohne Operation nur 1 Versterben (10 % von 11 Erkrankten), während 10 Erkrankte, die operiert werden, von einem solchen Eingriff nicht profitieren, also sozusagen umsonst operiert werden.
Da der Chirurg jedoch nicht weiß, welcher seiner 11 zu operierenden Erkrankten derjenige ist, welcher am wahrscheinlichsten stirbt, muss er alle 11 Erkrankten operieren, um diesen einen auch „zu erwischen“, den er damit retten kann. Da mit dem neuen Eingriff auch Komplikationen einhergehen, bis hin zu Versterben an den Folgen der Operation, wird die Wirksamkeit insgesamt erheblich „verwässert“ und es werden Erkrankte, die wahrscheinlich die Erkrankung problemlos überstanden hätten, einem zusätzlichen und vermeidbaren Risiko zugeführt, ohne von dem Eingriff einen Nutzeffekt erwarten zu können.
Zusammengefasst bedeutet dieser geschilderte Zusammenhang: Je höher die Zahl notwendiger Eingriffen oder verabreichter Medikamente, um einen Erfolg zu erzielen, um so größer ist die Zahl vermeidbarer unerwünschter Nebenwirkungen und die Zahl derjenigen, die „umsonst“ behandelt werden.
Was ist an dieser Stelle zu tun?
Etwas, was in unserem Beispiel bereits vor der Zulassung der neuen Methode durch die Kommission hätte erfolgen müssen: Zu klären, welche Gruppe von Erkrankten denn überhaupt am meisten von der neuen Methode profitiert und ob es überhaupt notwendig ist, alle Erkrankten zu operieren.
Anders und medizinisch ausgedrückt: Welche Parameter des Krankheitsverlaufs und der bisherigen Beobachtung der Erkrankten geben mir einen Hinweis, um folgende Fragen zu beantworten:
Gibt es unterschiedliche Verläufe der Erkrankung beispielsweise im Verhältnis zum Lebensalter der Erkrankten?
Gibt es Gruppen von Erkrankten, denen wir mit den bisherigen Mitteln kaum oder nicht genügend helfen können und die besonders häufig an dieser Erkrankung sterben, so dass dann eine neue Methode trotz der relativ hohen Zahl von möglicherweise „umsonst“ operierten Erkrankten davon profitieren würde?
In unserem Beispiel gäbe es auch nach einer breiten Anwendung dieser Methode noch eine Möglichkeit, diese Erkenntnisse zumindest näherungsweise aus den für die Zulassung eingereichten Daten des Chirurgen zu entnehmen, indem die Kommissionsmitglieder sich die Mühe machten, beispielsweise die Alterstruktur oder die Nebenerkrankungen der in den einzelnen Gruppen enthaltenen Erkrankten anzuschauen.
Zurück zur Statistik
Das Beispiel demonstriert, auf welche Weise es gelingt, Ergebnisse von Studien zur Wirksamkeit von Methoden oder Medikamenten möglichst wirkungsvoll zu präsentieren; ganz legal, ohne Fehlberechnung oder irgendwelche Unterschlagungen.
Die Konsequenz ist klar: Jeder, der sich mit den Ergebnissen von Studien zu medizinischen Sachverhalten beschäftigt, die ein mittels Zahlen gefasstes Ergebnis enthalten, ist gut beraten, genau nachzuschauen, ob eine relative oder absolute Ergebnisangabe erfolgte und wie hoch die Anzahl derjenigen ist, die mit einer bestimmten Methode oder einem Medikament behandelt werden müssen, um 1 Erfolg zu erzielen und diese Zahl dann zu dem eigentlichen Risiko einer Erkrankung in Relation zu setzen.
Im Übrigen trifft das nicht nur für medizinische Studien zu, sondern für nahezu jede Darstellung in den verschiedenen Medien, den Nachrichten und durch politische Akteure.
Seien Sie wachsam, rechnen Sie nach und vor allem: Machen Sie sich Ihr eigenes Bild.
Die Ausarbeitung erfordert die ‚Note‘
sehr gut .
Die Professoren an der Fakultät für Statistik der TU Dortmund würden sich ganz klar über
eine derartige Ausarbeitung freuen.
Hallo Herr Eichweber,
vielen Dank für die freundliche Anerkennung. Ich hoffe, es hilft dem einen oder anderen, zu verstehen…